构建可复制的成全式教育生态
写在前面：
数学作为三大学科之一，可能是最让家长忧愁、孩子痛苦的一个学科。学好数学对孩子的思维发展尤其重要，所以，一直以来，家长们对孩子的数学学习也极度关注。
今天这篇文章，来自对一土数学老师、数学教研组组长芳杰老师的采访，回答了很多我们关心的数学话题：● 什么样的方式才能让孩子更好地积累数学活动经验？Ivy：作为一土的数学老师，您怎么看待数学这门学科？通过数学我们希望培养孩子的什么品质或者能力？芳杰：作为一土学校课程育人中的一部分，数学学科与其他学科相较，既有共性同时也有它的个性。共性的地方体现在，我们共同的育人目标都是在培养“内心充盈的乐天行动者，理性创新的高效学习者”。个性的地方则在于，“从学生长期发展来看，数学除了知识和技能的学习，从学科育人的角度看，我们更希望通过数学的学习帮助学生学会思维。”需要澄清的一点是上面提到的“思维”具有更加广义的理解，并不仅仅局限于“数学思维”的名词含义，还包含了动词含义。就像数学家波利亚特别强调的“问题解决”，他致力于研究的“数学启发法”中的方法或原则就具有这样更为普遍的意义，即“不限于任何题目”。
▲ 小土豆在课堂上讲解如何解决这个数学问题
那么作为数学老师，我们要区分好数学和数学教育。数学教育者要做的是充分发挥数学学习对于学生理性思维培养方面的积极意义，真正地为学生们，无论未来是从事数学相关工作还是其他工作的学生们做些什么，让他们具备面对未来的能力和素养。就像史宁中教授所言的那样“数学教学的最终目标，是要让学习者会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。而数学的眼光就是抽象，数学的思维就是推理，数学的语言就是模型。”芳杰：首先，我们要辩证的来看什么叫“学好数学”。因为并不是每个孩子都会长线的去研究数学或者从事与数学相关的工作。数学和数学教育是两回事。在这里不展开说。作为一名数学教育工作者，我们要做的就是以数学教育为载体，为每一个孩子插上思维的翅膀，作为一个公民，具备面对未来世界的基本能力和素养，这是我们对“学好”的基本标准。那作为学习者，学校的数学教育只是他数学学习的一部分。如果一个孩子对数学是特别感兴趣的，特别愿意研究它，对这个孩子来讲，“学好”就没有上限标准。数学教育作为学校教育的一部分，学好数学最重要的是孩子的好奇心和求知欲，也就是当他面对问题时，是否具备问题解决的思维，一个外显的表现就体现在“会不会不断地发问”。
Ivy：面对“发问”这项关键能力，当有孩子提出问题的时候，我们作为教育者会怎样引导孩子去建立理性思维？芳杰：我们特别鼓励孩子提出问题，并让他们不断获得“提出问题是好事儿，很了不起”的正向反馈。但是作为教育者，我们知道提出问题的能力不能只停留在把问题提出来，要引导孩子们就提出的问题继续进行思考，并做出初步的猜想。当孩子们给出多个猜想的时候，鼓励他们从某一个猜想开始，联系自己已有的知识和经验，一步步继续往下想，慢慢的孩子就会不断把他的生活经验以及之前积累的与数学相关的经验联系起来。开始的阶段很重要，需要老师不断的给予帮助和支持。当然，除了鼓励和引导，方法和工具也很重要，比如电子设备，一些适合的app或者网上搜索的资料，各种各样的图书等……作为教育者，我们会通过一定的教学设计，让孩子经历“观察、猜想、假设、验证、得出结论”或“再观察、再猜想、再假设、再验证”……这一“发现问题提出问题、分析问题解决问题、评价与反思”的完整问题解决的过程，在“验证失败，再猜想”或“验证成功，得到结论”的过程中，不断的积累数学活动经验，同时慢慢地建立这样的问题解决的思维方式。在面对“未知”时，孩子才会越来越敢想敢问、敢猜想，并有方法去验证。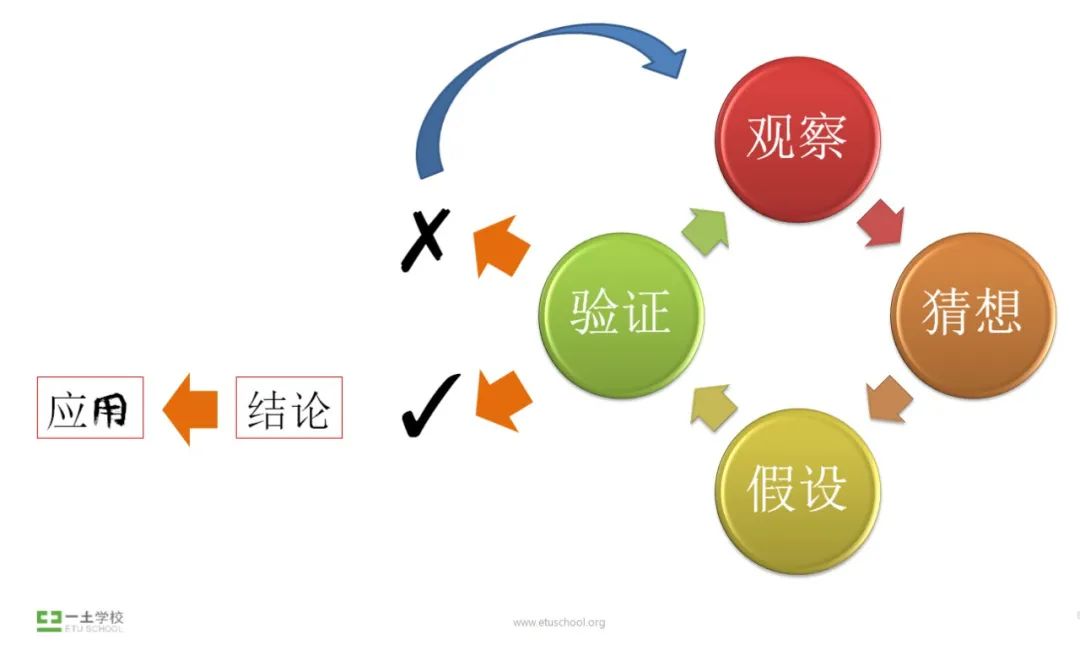
▲ 图片来自芳杰老师
当然问题解决能力的培养不是一蹴而就的。例如针对不同年龄段的孩子，老师们会将“观察、猜想、假设、验证”、 “再观察、再猜想、再假设、再验证”的步骤进行拆解，辅以相应的学习载体，尤其是对低龄段的孩子，绝不能一股脑儿的丢给孩子，那样对孩子来讲太难了！数学学习的内容从深度和广度上是一条螺旋上升的线，同时，孩子的认知发展也是一条螺旋线，这两条螺旋线一定是要相辅相成的。数学学习内容的设置符合儿童的认知发展规律，数学教育以这些内容为载体，发展学生的能力与素养，同时学生认知能力的发展也会带动对学习内容的需求，两条螺旋线彼此推动，螺旋往上走。所以，为什么要区分数学和数学教育？数学教育就是要把这两条线揉到一起，内容线和儿童发展的这两条线是彼此互相推动的，而不是说单独看一条线的发展。无论是单独看内容的线，还是单独看儿童认知发展的线，都不足以很好地事半功倍地落实数学教育的目标。所以从数学教学的实践来讲，应该是“双轨的”。Ivy：在具体的教学实践中充分尊重并遵循双螺旋的发展规律，为教者的功夫是非常重要的。针对这个双螺旋我们的教学是如何开展的？芳杰：是的，如何进行引导、激发、鼓励，借助怎样的形式，将数学的知识、技能、思想方法等从教育者或学习载体中传递给学习者，老师的角色非常重要。不同的年级，对教师的要求也不同。数学学科对一二年级的数学老师要求非常高，尤其是一年级的老师。一年级的老师们要从学前的思维启蒙衔接到小学的数学学习，双轨意识就非常重要。很多看不到的功夫，都在老师们的教学设计中，像学生前测、分析、学习内容分析，活动设计等。一直到三年级之前，会有大量的基础内容的输入，比如：基础知识、基本技能的获得、基本思想方法的领悟和基本数学经验的积累等。老师要处理好“教与学的关系”，“教与扶、放手让学生探究”的次序、比重等。我们最终的目的是希望学习者能自主推动“个体认知发展与数学内容线”的发展，而不是一味地由教育者在牵引这条线走。所以，到了三年级，老师们会动态地调整“教与扶、学生自主探究”的次序、比重等，教师角色也将“教”的比重向“教练”的角色偏移一些。在学习的过程中，不再给学生特别多的拐棍了，因为他已经有了方法，两条腿越来越有力量，能自己站住，自己往前走了，慢慢过渡到自主学习的高年段。这一阶段教师更多的不断引导学生发现新旧知识之间的关联，借助对比和联系，逐步构建不同板块数学内容的逻辑线。从学习方式上，在自主学习的同时，逐步从两人合作学习过渡到四人合作探究学习，引导学生观察、思考、摸索适合自己的学习方式。
所以对中年级的老师要求也很高，他们一方面要扎实推进教与学的角色切换，另一方面也要根据学生的认知发展，提供个性化支持，帮助一些还没有顺利过渡的学生实现从低年级到中年级的过渡。
芳杰：高年级的老师更多的会在思维的灵活性和创新方面给予更多的引导，给学生自主学习、合作学习的空间会更大。这一阶段教师会继续引导学生主动发现新旧知识之间的关联，通过归纳概括、重构、梳理数学知识的版图，通过设置挑战性问题，独立思考与同伴合作学习并重，鼓励并引导学生综合运用已有的学习经验，多角度思考、方法灵活、多样化。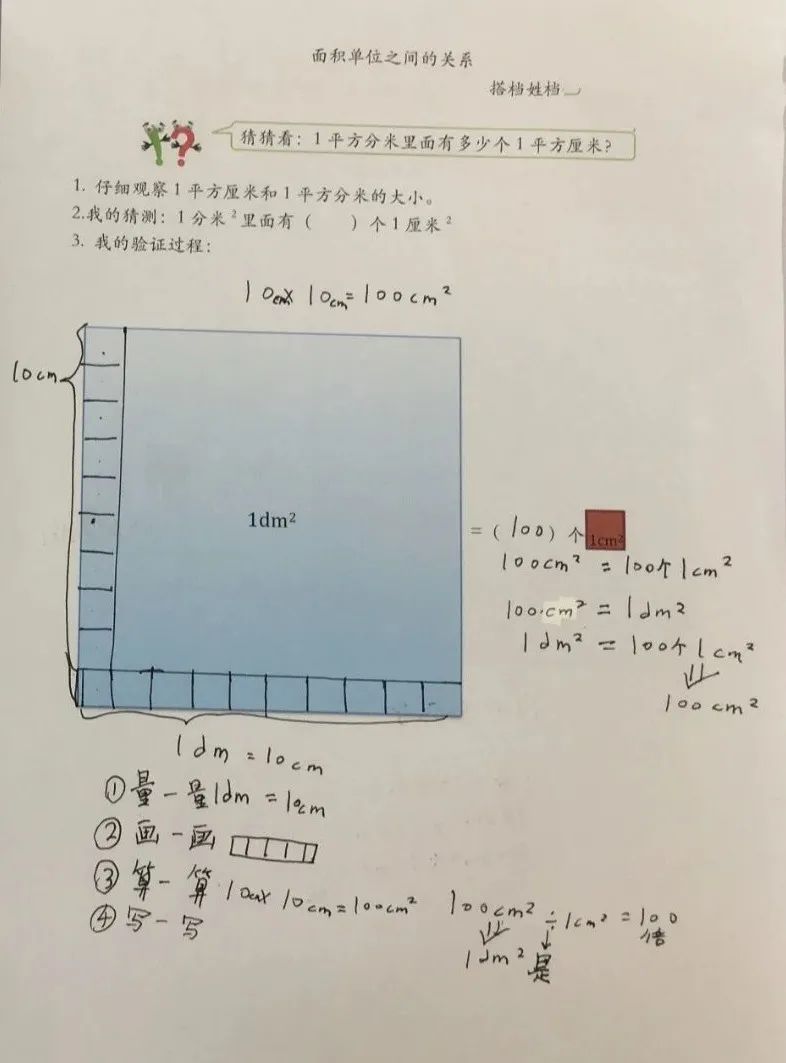
▲ 多角度思考，分析推理验证“面积单位之间的进率”
▲ 方法灵活、多角度地解决问题
和中年级老师一样，有些孩子虽然上了高年级，但认知发展还没有达到高年级的水平，这就需要充分发挥同伴学习的力量和个性化学习内容的设置，以帮助这些孩子完成从中年级到高年级的过渡。在这个过程中，“主动学习的内驱力”依然必不可少，只有学生借助自己的力量不断地克服一个又一个挑战，才能不断地获得成就感，能力和素养才真的在他的身上生根发芽。 直观教学活动经验的积累，影响孩子后续抽象思维的发展 Ivy：如果到了三年级，孩子还不能独立探索，除了知识技能的匮乏之外还有没有其他原因？芳杰：有的，除了基础知识和基本技能的不扎实，还有基本思想方法的理解和基本数学活动经验积累的匮乏。可能在之前的学习中，更多的关注了结果而忽略了过程，知其然却不知其所以然。例如数学的抽象思维培养，离不开大量的直观数学活动经验的积累，尤其是低年级的数学学习，经常有三四年级的家长说，“我给他摆一摆，画一画他就明白了，但自己就是想不明白。”说的就是这个道理。
▲ 一年级小土豆在课堂上画一画
比如说像一年级，在一土的课堂中，会有大量的直观学具的引入，像圈一圈、画一画、摆一摆，说一说，尤其这种摆一摆，就是在帮他积累数学活动经验，经历从直观到抽象的过程。最重要的是还要经历从抽象再次回到直观的过程。
▲ 一年级小土豆在课堂上圈一圈
如果没有这样的从直观到抽象，从抽象再次回到直观的学习过程，直接进行抽象的数量关系学习，有一部分孩子就会不理解。在一二年级的学习过程中，老师会通过情境创设或者内容载体设计，在课堂当中，通过让孩子与同伴、与学习内容，以及在自身学习过程当中，不断地将知识技能、思想方法和活动经验进入到思维体系里面，日积月累。到了三年级，有一部分同学自然就能调用出来，还有一部分同学不能调用，针对不能调用的这部分同学，老师会具体分析他们的原因，是原本就没有这些经验的积累还是积累了经验但不能调用。Ivy：其实圈一圈、画一画这类就是不同的数学语言。能深入的说一下这些活动经验对学习数学的意义在哪里吗？尤其是对小学高年级段的孩子。芳杰：是的，这就谈到了数学的多种语言表征。在数学语言中中，有动作语言、符号语言、文字语言，还有图表语言等，这几种数学语言从数学启蒙阶段就开始不断地切换使用了。抽象的符号、图表语言的表达不是一蹴而就的，随着低年级到中年级的发展，符号语言开始被大量的使用，用符号进行关系表征，是从算术到代数发展的重要标志。就像华罗庚先生所说的“数缺形时少直观，形缺数时难入微”。圈一圈画一画的方法，无论是小学的低年级还是高年级都非常重要，它是帮助思考、分析、理解的工具，是辅助表达想法的一部分。处于不同认知发展阶段的孩子都可以很容易拿起来用的工具。例如有些同学能背下来公式，却不懂背后的道理，无法完成迁移和运用。越到高年级学习起来就会越困难。所以作为教育者，需要不断给孩子这种直观的工具支撑，在探究活动当中去让处于不同认知发展阶段的孩子得到发展，完成抽象、归纳、概括的过程。
数学的学习一定是知其然还要知其所以然。比如我们三年级正在讲乘法，很多孩子在上这个课之前，就已经能够用乘法数式竖式来计算。但是当我去追问为什么要这样写乘法数式时，孩子们会说我妈妈（爸爸）就是这么教我的。当我追问“你能解释一下竖式中这一步表示什么意思？”时，发现很多孩子都是不知道的。
这个所谓的“意思”在数学上称之为“算理”。对算理的理解，从一年级到六年级都是贯穿始终的，都可以借助摆一摆、圈一圈、画一画的方式来理解。
以“乘法”的板块学习为例，二年级乘法的初步认识，三年级开始多位数乘一位数，后续会陆续学习多位数乘多位数、小数乘法、分数乘法等，在整个乘法学习的过程中，关于乘法最开始的思维结构搭建好至关重要！摆一摆、圈一圈、画一画为他们提供了最初的乘法结构的直观经验，从直观到抽象概括过渡。后续的乘法学习不过是不断地把这个结构细化，把模型进行调整。
▲ 三年级两位小土豆在课堂上，借助学具摆一摆，分享多位数乘一位数乘法口算算理算法
▲ 三年级小土豆数学思考分享：画一画分析，抽象的算式符号表达解决问题中高年级老师的挑战点在于：借助问题和情境的设置，给不同发展阶段的孩子“亡羊补牢”的机会。在每一次新螺旋开始时，老师们都会带孩子去整体回顾已经具备了什么，每个孩子个体的结构库里面都有什么。即KWL中的“K”（我已经知道的）。每个年段的数学老师都非常重视前测。针对班级学生的学习基础，设计班级的教学，对学生而言，前测也是让他自己知道自己的知识库里已经有什么，怎么有结构的整理自己的知识库等？比如加法结构到乘法结构的建立。虽然二年级时就学完了乘法，但并不是所有的孩子都从加法结构过渡到了乘法结构。数的认识、数的计算与形的发展相辅相成，例如想到24，它可以是1×24 ，2×12，,3×8，4×6等，对应的可以是“一维的线”结构，也可以是“二维的面”结构。而到了五年级就该有“体”出现，1×1×24，1×2×12，2×2×6等，三维结构就要来了，所以始于“摆一摆、圈一圈、画一画”的直观方式，终于抽象的符号与结构表征。“摆一摆、圈一圈、画一画”搭建起了直观与抽象之间的桥梁。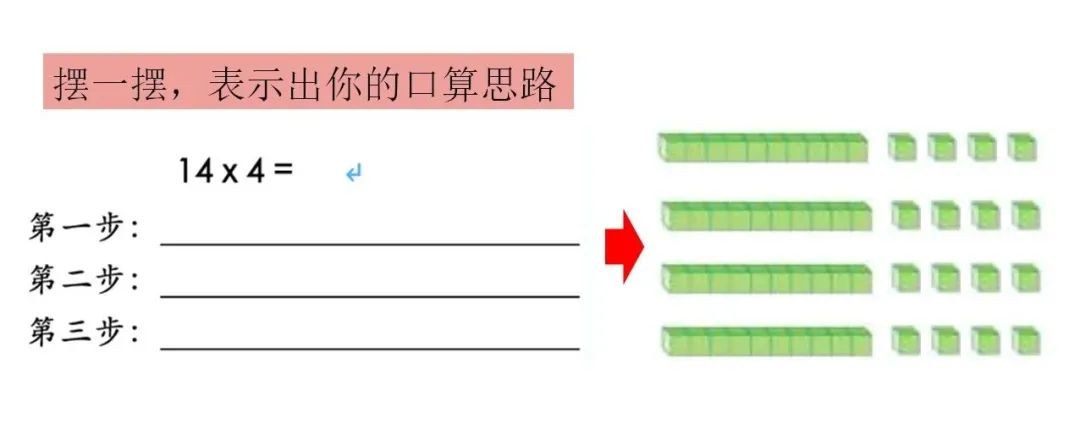
Ivy：如您所说，数学的结构思维启蒙是至关重要的，但在实施的过程中怎么做到和效率之间的平衡？ 芳杰：每个年级都有要抓的重点，老师从备课的角度上，会基于本年级所处的位置，学生的基础、学习内容的重点来进行取舍。比如，低年级的老师不会过分地去引导“你很聪明”，而是不断的正向引导“你怎么那么会听，你怎么那么会想。你怎么那么会表达啊”，还要让他知道“我怎么会听的，我怎么会想的，我都是怎么表达的”这种对元认知思考的培养。
▲ 一土三年级的同学在向全班分享自己的数学思考，同学们听懂后打出666的手势表示赞同（听懂）这样的引导和培养从入学就开始，而不是说等到三年级，我们才去让孩子去学习评价和反思。从他开启数学学习的那天，我们努力让孩子知道他打开的是一扇数学的大门，这扇大门背后有无限可能，而且这扇大门跟任何一扇大门都不一样。Ivy：好的，最后一个问题也是代表了很多家长的焦虑，那就是关于幼小衔接，您觉得对数学这个科目来讲，要不要提前学习？芳杰：现在市面上有很多关于幼小衔接方面的资源或课程。首先要澄清“幼小衔接VS思维启蒙”、“思维启蒙VS数学知识学习”。以我的个人观点，同时结合带我姐姐的女儿学习的经验来看，幼小衔接训练的课程内容如果是特别指向抽象的数的运算的，其实没有太多的必要。幼小衔接的数学部分包含哪些内容，具体可以参考3~6岁儿童学习与发展指南中的数学板块。比起具体的知识的学习，幼小衔接首要重要的是自我管理的能力，尤其是生活自理能力，比如能够自己照顾自己，穿衣服，系鞋带等，有规律的作息，基本的收纳习惯等等。还有一点特别重要，就是尽量多地亲近自然，尤其是男孩子，充分地去释放天性，上了小学之后，孩子玩儿的时间都会有所减少，在疯玩之余，附带着在亲近自然中积累“日常数学”经验。
▲ 多亲近自然
孩子空间感的构建，不单纯是闷头在家里搭乐高能出来的，更不要迷信于低头作业。比如让孩子出去跑一跑，看一看远处的东西，用一步、一拃、一庹实际去丈量，对将来长度这一量感的发展，很有帮助。有人可能到了十几二十岁，都没有100米有多远的概念。很多孩子的空间感、量感的发展不全是老师教的，更多的是“日常数学”经验的积累和学习经验的积累得到的。比如我拿起一个手机，就知道这个绝对没有1千克，这个标准是什么，可能是一盒800克的曲奇饼干。这都是生活经验的积累，而不是老师告诉你这个东西有20千克，你记住它有20千克就可以了。说这些可能还是没有完全地缓解家长们的一些顾虑，如果家长对幼小衔接阶段的思维启蒙这部分比较有研究，同时也有充分的时间可以陪孩子，可以与孩子进行一些有关量的认识、数的认识、数的运算、逻辑推理等数学游戏。（温馨提示：一定要有情境（讲故事）、有学具操作，可以参考一些数学绘本，以此为骨架来设计与孩子的亲子活动。每个孩子都是爱听故事的，也是喜欢做游戏的，思维启蒙包裹上“故事和游戏”的糖衣，相信没有孩子不喜欢吃哦！）所以，幼小衔接阶段，还是要让孩子多去经历和感知，在生活中、在自然中、游戏中去学习，积累“日常数学”的活动经验，以这些经验为标准，在未来过渡到“学校数学”的系统化学习时，调用和迁移经验就会容易得多。千万不要舍本逐末，过分地追逐具体知识的学习。
写在后面：
其实每个孩子都有用数学的眼光看世界的能力，也拥有用数学的思维辩证分析的潜力。
一土芳杰老师说，数学课程作为学校整体课程中的一部分，是以知识技能为载体，在不同内容领域知识技能系统化、结构化的过程中，感悟数学思想方法、积累活动经验，从而实现学生知识技能、数学思考、问题解决和情感态度四个不同维度目标的发展。
如果把数学学习比作一块田，知识技能的学习就相当于不同区域划分的农作物，如何耕耘，对果实有怎样的期待，所体现的就是我们的课程实施过程、方法和课程育人目标。
|
|
想更深入了解一土学校小学部的详细信息，欢迎您参加1月24日上午10:00的小学部线上说明会（参与详情见下方海报）。
待疫情好转后，我们会组织线下探校活动，让对一土学校有兴趣的家长充分了解最真实的一土，便于大家申请2021年度的学位。本次线上说明会您可以了解到一土这所学校到底有什么不一样？我们培养的是什么样的人？我们还安排了课程体系的介绍，教学与评估的分享，还有现任大土豆现身说法以及答疑时间，期待与您线上相见！ |
▫ 偶尔留言，哪怕跟我们say个hi~
▫ 时不时点一下”在看“和”赞“，或点”分享“给需要的朋友
